SVM总结¶
- 支持向量机在解决小样本、非线性及高维模式识别问题中表现出了许多特有的优势,针对多类分类问题的经典SVM 算法主要有一对一方法(1-vs-1),一对多方法(1-vs-all.
线性可分问题¶
- SVM 是从线性可分情况下的最优分类面发展而来的,所谓最优分类面就是要求分类面不但能将两类样本正确分开(训练错误率为0),而且使分类间隔最大.设有n 个样本xi 及其所属类别yi 表示为:

超平面W·X+b=0 方程,能将两类样本正确区分,并使分类间隔最大的优化问题可表示为在式的约束下求下式最小值.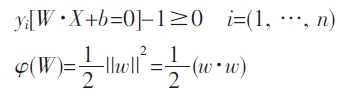
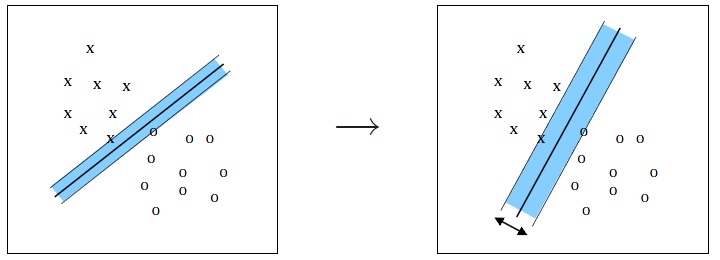
满足条件且使||w||2 最小的分类面就是最优分类面. 过两类样本中离分类面最近的点且平行于最优分类面的超平面上的训练样本就是第一个式子中使等号成立的那些样本,它们叫做支持向量. 因为它们支撑了最优分类面.
线性不可分问题¶
- 最优分类面是在线性可分的前提下讨论的,在线性不可分的情况下,就是某些训练样本不能满足第一个式子的条件,因此可以在条件中增加一个松弛项,此时约束条件变为:

式中的C 为某个指定的常数,起到对错分样本惩罚程度控制的作用,实现在错分样本的比例和算法复杂程度之间的“折衷”. 该问题可转化为其对偶问题.
这是一个不等式约束下二次函数极值问题,存在唯一解. 求解出上述各系数α、W、b 对应的最优解α*、W*、b*后,得到最优分类函数
非线性问题¶
- 现实问题几乎都是非线性可分的,对非线性问题,可以通过非线性变换转化为某个高维空间中的线性问题3,在变换空间求最优分类面. 根据泛函的有关理论,只要一种核函数k(x, xi)满足Mercer 条
件,它就对应某一变换空间中的内积. 因此,在最优分类面中用适当的内积核函数k(x, xi)就可以实现从低维空间向高维空间的映射,从而实现某一非线性变换后的线性分类,而计算复杂度却没有增加.
多类SVM 分类算法分析与研究¶
一对一支持向量机(1-vs-1 SVM)¶
- 一对一支持向量机(1-vs-1 SVM)[2]是利用两类SVM 算法在每两类不同的训练样本之间都构造一个最优决策面. 如果面对的是一个k 类问题,那么这种方法需要构造k(k-1) / 2 个分类平面(k>2). 这
种方法的本质与两类SVM 并没有区别,它相当于将多类问题转化为多个两类问题来求解. 具体构造分类平面的方法如下:
从样本集中取出所有满足yi=s 与yi=t (其中1燮s, t燮k, s≠t)通过两类SVM 算法构造最优决策函数用同样的方法对k 类样本中的每一对构造一个决策函数,又由于fst(x)=-fts(x),容易知道一个k 类问题需要k(k-1) / 2 个分类平面.根据经验样本集构造出决策函数以后,接下来的问题是如何对未知样本进行准确的预测. 通常的办法是采取投票机制:给定一个测试样本x,为了判定它属于哪一类,该机制必须综
合考虑上述所有k(k-1)/2 个决策函数对x 所属类别的判定:有一个决策函数判定x 属于第s 类, 则意味着第s 类获得了一票,最后得票数最多的类别就是最终x 所属的类别.
- 1-vs-1 SVM 方法,优点在于每次投入训练的样本相对较少,因此单个决策面的训练速度较快,同时精度也较高. 但是由于k 类问题需要训练k(k-1) / 2 个决策面,当k 较大的时候决策面的总数将过多,因此会影响后面的预测速度. 这是一个有待改进的地方. 在投票机制方面,如果获得的最高票数的类别多于一类时,将产生不确定区域;另外在采用该机制的时候,如果某些类别的得票数已经使它们不可能成为最终的获胜者,那么可以考虑不再计算以这些类中任意两类为样本而产生的决策函数,以此来减小计算复杂度.
一对多支持向量机(1-vs-all SVM)¶
- 一对多支持向量机(1-vs-all SVM)[4]是在一类样本与剩余的多类样本之间构造决策平面,从而达到多类识别的目的. 这种方法只需要在每一类样本和对应的剩余样本之间产生一个最优决策面,而不用在两两之间都进行分类. 因此如果仍然是一个k 类问题的话,那么该方法仅需要构造k 个分类平面(k>2). 该方法其实也可以认为是两类SVM 方法的推广. 实际上它是将剩余的多类看成一个整体,然后进行k 次两类识别. 具体方法如下:
- 假定将第j 类样本看作正类(j=1, 2, …, k),而将其他k-1 类样本看作负类,通过两类SVM 方法求出一个决策函数, 这样的决策函数fj(x)一共有k 个. 给定一个测试输入x,将其分别带入k 个决策函数并求出函数值,若在k 个fj(x)中fs(x)最大,则判定样本x 属于第s 类.
- 1-vs-all SVM 方法和1-vs-1 SVM 相比,构造的决策平面数大大减少,因此在类别数目k 较大时,其预测速度将比1-vs-1 SVM 方法快. 但是由于它每次构造决策平面的时候都需要用上全部的样本集,因此它在训练上花的时间并不比1-vs-1SVM 少. 同时由于训练的时候总是将剩余的多类看作一类,因此正类和负类在训练样本的数目上极不平衡,这很可能影响到预测时的精度. 另外,与1-vs-1 方法类似,当同时有几个j 能取到相同的最大值fj(x)时,将产生不确定区域。